Continuous Piecewise Linear Mixed Effects Model Using R

I often get asked how to fit different multilevel models (or individual growth models, hierarchical linear models or linear mixed-models, etc.) in R. In this guide I have compiled some of the more common and/or useful models (at least common in clinical psychology), and how to fit them using nlme::lme() and lme4::lmer(). I will cover the common two-level random intercept-slope model, and three-level models when subjects are clustered due to some higher level grouping (such as therapists), partially nested models were there are clustering in one group but not the other, and different level 1 residual covariances (such as AR(1)). The point of this post is to show how to fit these longitudinal models in R, not to cover the statistical theory behind them, or how to interpret them.

Data format

In all examples I assume this data structure.

subjects	tx	therapist	time	y
1	0	1	0	10
1	0	1	1	12
1	0	1	2	14
2	0	1	0	4
2	0	1	1	14
2	0	1	2	13
3	0	2	0	12
3	0	2	1	15
3	0	2	2	16
4	0	2	0	17
4	0	2	1	13
4	0	2	2	12
5	0	3	0	15
5	0	3	1	13
…	…	…	…	…

Where subjects is each subject's id, tx represent treatment allocation and is coded 0 or 1, therapist is the refers to either clustering due to therapists, or for instance a participant's group in group therapies. Y is the outcome variable.

Power analysis, and simulating these models

Most of the designs covered in this post are supported by my R package powerlmm, (http://cran.r-project.org/package=powerlmm). It can be used to calculate power for these models, or to simulate them to investigate model misspecification. I will soon integrate the package into this post, in order to create example data sets. For now, see the package's vignettes for tutorials.

Longitudinal two-level model

We will begin with the two-level model, where we have repeated measures on individuals in different treatment groups.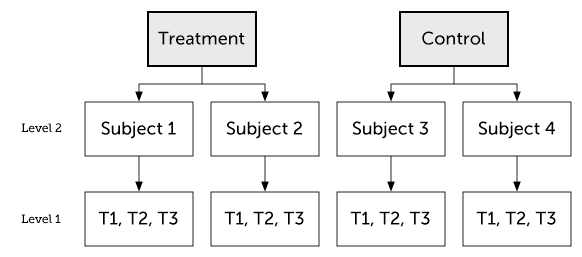

Unconditional model

Model formulation

with,

and

To fit this model we run

Unconditional growth model

Model formulation

with,

and

To fit this model we run

Conditional growth model

Model formulation

with,

and

To fit this model we run

Conditional growth model: dropping random slope

Model formulation

with,

and

To fit this model we run

Conditional growth model: dropping random intercept

Model formulation

with,

and

To fit this model we run

Conditional growth model: dropping intercept-slope covariance

Model formulation

with,

and

To fit this model we run

Three-level models

Here I will cover some different three-level models. In my examples clustering at the highest level is due to therapists. But the examples generalize to other forms of clustering as well, such as group therapy or clustering due to health-care provider.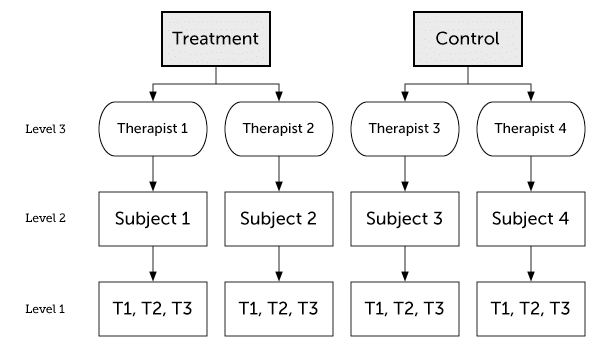

Conditional three-level growth model

We will jump straight to the conditional three-level growth model, with the following model formulation:

with,

and,

and

To fit this model we use therapist/subjects, which specifies nesting. This formula expands to a main effect of therapist and a interaction between therapist and subjects (which is the subject level effect).

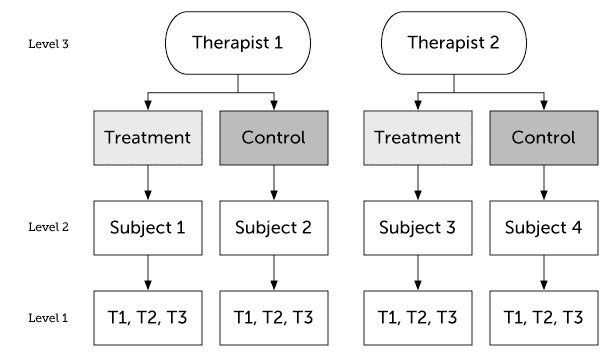
Subject level randomization (therapist crossed effect)

In the previous example therapists only provided one type of treatment (nested design). Sometimes therapists will be a crossed effect, i.e. in a parallel group design they will deliver both treatments. If it's a randomized trial then in this design we have subject level randomization, whereas in the previous example randomization was at the therapist level.

with,

and,

and

In this model we estimate no covariances at level 3. However, at the therapist level we have random effects for time, treatment and time treatment*. I fit this saturated model because you can easily delete a random effect in the expanded lmer syntax below.

Different level 3 variance-covariance matrix

We might hypothesize that therapists that are allocated participants that report worse symptoms at treatment start have better outcomes (more room for improvement). To allow for separate covariances in each treatment group we update the variance-covariance matrix at level 3

To fit this model we run

Of course, we could also estimate all six covariances at level 3. For instance, we could look at if therapists who are more successful with Treatment A are also more successful with Treatment B, i.e. , and so forth. The full unstructured level 3 variance-covariance matrix we will estimate is thus

Which we fit by running

Partially nested models

Partially nesting occurs when we have nesting in one group but not the other. For instance, we might compare a treatment group to a wait-list condition. Subjects in the wait-list will not be nested, but subjects in treatment group will be nested within therapists.

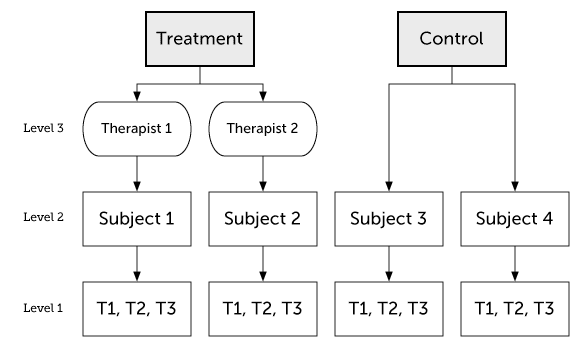
We can write this model like this

with,

and,

and

More on level 1 specification

Heteroscedasticity at Level 1

Only lme allows modeling heteroscedastic residual variance at level 1. If we wanted to extend our two level model and allow for different level 1 residual variance in the treatment groups, we'd get

If we wanted to extend our two-level model with this level 1 structure we'd run

More grouping

We could also add another grouping factor such as time, and fit a model with heteroscedastic level 1 residuals for each time point in each treatment group. For instance, for i = 0, 1, 2 we get

which we'd fit by running

First-order Autoregressive AR(1) residuals

For time points we get the level 1 variance-covariance matrix

we leads to

To fit this level 1 residual structure we use the correlation argument.

Heterogenous AR(1)

We can also extend the level 1 variance-covariance matrix from above, to allow for different residuals at each time point.

and we have that

To fit this level 1 model we simply use both the correlation and the weights argument.

More level 1 variance-covariances matrices

Se ?corClasses for the different types of residual variance-covariances matrices lme can estimate.

Changing the functional form of time

All of the examples above assume linear change. Here I will cover some examples of how to model nonlinear change at level 1. The examples will be based on the two-level model, but you could easily be combined them with the three-level models outlined above.

Quadratic trend

with,

and

Orthogonal polynomials

If you'd like to fit orthogonal polynomials you can use the poly() function with raw = FALSE (which is the default).

Piecewise growth curve

Segmenting the time trend into different pieces has got more to do with simple dummy coding of regression variables, than any specifics of lme or lmer. However, I will cover some common scenarios anyway.

To fit a piecewise growth model we simply replace time with two dummy variables time1 and time2, that represent the different time periods. A common scenario is that the first piece represents the acute treatment phase, and piece 2 represent the follow-up phase.

Coding scheme 1: separate slopes

Time	0	1	2	3	4	5
Time 1	0	1	2	2	2	2
Time 2	0	0	0	1	2	3

Coding scheme 2: incremental/decremental slope

Time	0	1	2	3	4	5
Time 1	0	1	2	3	4	5
Time 2	0	0	0	1	2	3

These two coding schemes only differ in the interpretation of the regression coefficients. In scheme 1 the two slope coefficients represent the actual slope in the respective time period. Whereas in scheme 2 the coefficient for time 2 represents the deviation from the slope in period 1, i.e. if the estimate is 0 then the rate of change is the same in both periods.

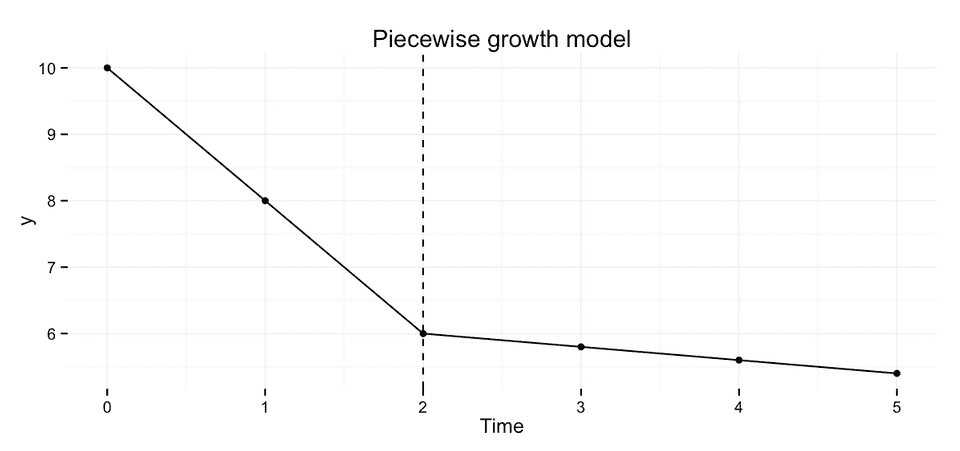
We could specify this model like this

with,

and

In this model I've fit the full level 2 variance-covariance matrix. If we wanted to fit this model we'd do it like this

Drop the correlation between time piece 1 and 2

Sometimes you might want to fit a model with a correlation between the random intercept and time piece 1, but no correlation between time piece 2 and the other effects. This would change the level 2 variance-covariance from above to this

Fitting this model is straight-forward in lmer and more complicated in lme.

Adding a quadratic effect

We could extend the two-part piecewise growth model to allow for non-linear change during one or both of the pieces. As an example, I'll cover extending the model to allow for quadratic change during piece 1.

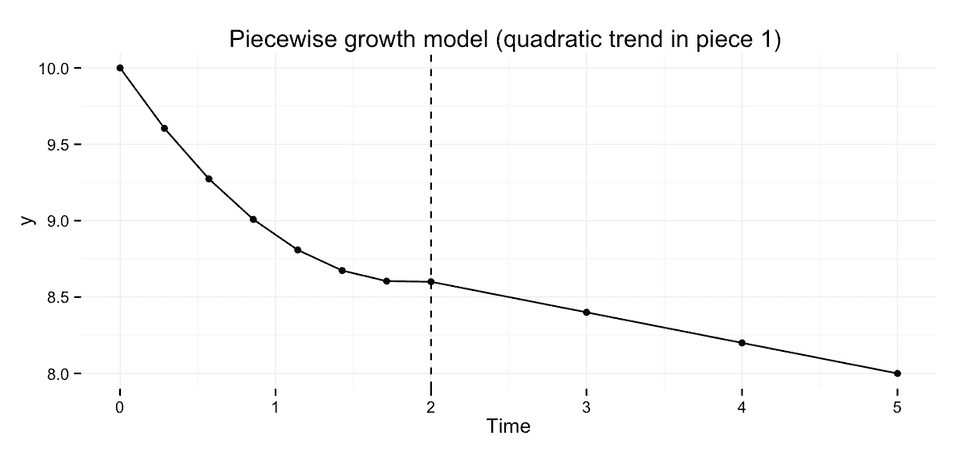
We could write this model like this

with,

and

This model could be fit like this

If you wanted to fit a reduced random effects structure you could use the method outlined in "Drop the correlation between time piece 1 and 2".

Hypothesis tests

lmer does not report p-values or degrees of freedoms, see ?pvalues and r-sig-mixed-models FAQ for why not. However, there are other packages that will calculate p-values for you. I will cover some of them here.

Wald test

Likelihood ratio test

Profile confidence intervals

Parametric bootstrap

Kenward-Roger degrees of freedom approximation

Shattertwaite degrees of freedom approximation

Book recommendations

Not all of these books are specific to R and longitudinal data analysis. However, I've found them all useful over the years when working with multilevel/linear mixed models.

Suggestions, errors or typos

Please don't hesitate to contact me if you find some errors in this guide.

davidhologe1980.blogspot.com

Source: https://rpsychologist.com/r-guide-longitudinal-lme-lmer/

Share this post